Choose Your Country or Region

Adrenergic Receptor

Isoform-selective Products

α-adrenergic receptor β-adrenergic receptor Beta-Adrenergic Receptor

Signaling Pathway

Adrenergic Receptor Products

All (168)
Adrenergic Receptor Inhibitors (20)
Adrenergic Receptor Activators (3)
Adrenergic Receptor Antagonists (67)
Adrenergic Receptor Agonists (76)
Adrenergic Receptor Modulator (1)
New Adrenergic Receptor Products

Catalog No.	Product Name	Information	Product Use Citations
S4009	Mirabegron	Mirabegron (YM 178) is a selective β3-adrenoceptor agonist with EC50 of 22.4 nM.	J Pers Med, 2022, 12(2)258 Hum Cell, 2022, 10.1007/s13577-022-00671-y Hum Cell, 2021, 10.1007/s13577-021-00639-4
S4076	Propranolol HCl	Propranolol HCl (AY-64043, ICI-45520, NCS-91523) is a competitive non-selective beta-adrenergic receptors inhibitor.	Cell Res, 2024, 10.1038/s41422-024-00946-z J Immunother Cancer, 2024, 12(11)e009805 Sci Rep, 2024, 14(1):4178
S2521	Epinephrine bitartrate	Epinephrine bitartrate (Adrenalinium) is an alpha- and beta-adrenergic receptor stimulator.	Sci Adv, 2024, 10(33):eado1533 Int J Biol Sci, 2023, 19(7):2006-2019 Int J Biol Sci, 2023, 19(7):2006-2019
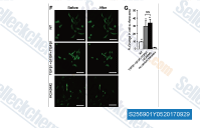
S2569	Phenylephrine HCl	Phenylephrine HCl is a selective α1-adrenergic receptor agonist, used primarily as a decongestant.	NPJ Regen Med, 2023, 8(1):9 Front Immunol, 2022, 13:1090773 Front Immunol, 2022, 10.3389/fimmu.2022.1090773
S2516	Xylazine HCl	Xylazine(BAY 1470 hydrochloride) is an α2-Adrenergic receptor agonist, used as a sedative and muscle relaxant.	J Immunother Cancer, 2024, 12(11)e009805 Cell Death Dis, 2023, 14(5):318 Eur J Pharmacol, 2021, 911:174522
S2507	Salbutamol (Albuterol) Sulfate	Salbutamol (Albuterol) Sulfate is a short-acting β2-adrenergic receptor agonist with an IC50 of 8.93 µM.	Front Physiol, 2022, 13:800055 cell, 2020, 180(1):64-78.e16 Sci Signal, 2020, 13(659)eaax0273
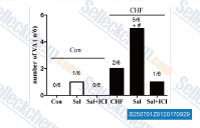
S1831	Carvedilol	Carvedilol (BM-14190, SKF 105517) is a non-selective beta blocker/alpha-1 blocker, used to treat congestive heart failure (CHF) and high blood pressure.	J Immunother Cancer, 2024, 12(11)e009805 Antioxidants (Basel), 2023, 12(8)1585 Antioxidants (Basel), 2023, 12(8)1585
S8114	Zenidolol (ICI-118551) Hydrochloride	Zenidolol (ICI-118551) Hydrochloride is a highly selective β2-adrenergic receptor antagonist with Ki values of 0.7, 49.5 and 611 nM for β2, β1 and β3 receptors, respectively.	Biomedicines, 2022, 10(2)487 iScience, 2021, 24(12):103362 Toxicol In Vitro, 2021, 77:105251
S2566	Isoprenaline (Isoproterenol) HCl	Isoprenaline (Isoproterenol) HCl is a non-selective beta-adrenergic receptor agonist, used for the treatment of bradycardia and heart block.	Stem Cell Res Ther, 2022, 13(1):287 BMC Cancer, 2022, 22(1):213 J Dairy Sci, 2022, 105-10:8426-8438
S1206	Bisoprolol fumarate	Bisoprolol fumarate (EMD33512) is a selective type β1 adrenergic receptor blocker.	J Immunother Cancer, 2024, 12(11)e009805 J Pathol, 2022, 10.1002/path.6020 Front Nutr, 2022, 9:907986
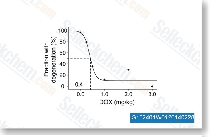
S1324	Doxazosin Mesylate	Doxazosin, a quinazoline-derivative, selectively antagonizes postsynaptic α1-adrenergic receptors, used in the treatment of high blood pressure and urinary retention associated with benign prostatic hyperplasia.	J Immunother Cancer, 2024, 12(11)e009805 J Exp Clin Cancer Res, 2023, 10.1186/s13046-023-02866-z J Ocul Pharmacol Ther, 2017, 33(1):50-56
S9507	(−)-Norepinephrine	(−)-Norepinephrine (Arterenol, Levarterenol, L-Noradrenaline) is a natural neurotransmitter and hormone. It is an agonist of adrenergic receptors with Ki values of 330, 56, and 740 nM for α1, α2, and β1 adrenoceptors, respectively.	iScience, 2023, 26(3):106241 Commun Biol, 2022, 5(1):339 Eur J Pharmacol, 2022, 926:175040
S2373	Yohimbine HCl	Yohimbine (Antagonil) has been used as a mydriatic and in the treatment of impotence. It is also alleged to be an aphrodisiac.	Anesth Analg, 2023, 137(2):426-39 Mol Pain, 2022, 18:17448069221107810 J Med Chem, 2021, 64(18):13510-13523
S1283	Asenapine maleate	Asenapine maleate (Org 5222) is a high-affinity antagonist of serotonin, norepinephrine, dopamine and histamine receptors, used for the treatment of schizophrenia and acute mania associated with bipolar disorder.	J Adv Res, 2024, S2090-1232(24)00079-1 Cell Commun Signal, 2024, 22(1):266 Mol Cancer, 2023, 22(1):136
S1549	Nebivolol hydrochloride (R-65824)	Nebivolol HCl (R-65824) selectively inhibits β1-adrenoceptor with IC50 of 0.8 nM.	J Immunother Cancer, 2024, 12(11)e009805 Oncogenesis, 2022, 11(1):24 Nat Commun, 2021, 12(1):5919
S2509	Sotalol HCl	Sotalol(MJ-1999) is a non-selective beta blocker and a potassium channel blocker with an IC50 of 43 μM.	J Immunother Cancer, 2024, 12(11)e009805 EBioMedicine, 2023, 95:104741 Toxicol Appl Pharmacol, 2021, 431:115731
S2090	Dexmedetomidine HCl	Dexmedetomidine HCl((+)-Medetomidine Hydrochloride) is a highly selective and potent alpha-2 adrenoceptor agonist, which reduces anesthetic requirements for patients by providing significant sedation.	Oral Dis, 2022, 10.1111/odi.14286 JHEP Rep, 2021, 3(4):100296 Sci Rep, 2021, 11(1):13345
S7974	L755507	L-755,507 is characterized as a potent and selective β3 adrenergic receptor partial agonist with EC50 of 0.43 nM. It is also recently identified to enhance CRISPR-mediated homology-directed repair (HDR) efficiency in human induced pluripotent stem cells (iPSCs) and other cell types.	Front Cell Dev Biol, 2023, 11:1276890 bioRxiv, 2023, 10.1101/2023.10.03.560773 Genesis, 2022, 60(1-2):e23465
S5739	Nebivolol	Nebivolol (Bystolic,R 065824) is a β1 receptor blocker with nitric oxide-potentiating vasodilatory effect used in treatment of hypertension and also for left ventricular failure.	Int J Mol Sci, 2023, 24(11)9708 Front Pharmacol, 2022, 13:1049640 Front Pharmacol, 2021, 12:691998
S5527	Salmeterol	Salmeterol (Astmerole, GR-33343X, SN408D) is a long-acting beta2-adrenergic receptor agonist with Ki value of 1.5 nM for WT β2AR and shows very high selectivity for the WT β2AR(β1Ki/β2Ki ratio of approximately 1500).	Front Pharmacol, 2022, 13:865715 Mol Syst Biol, 2021, 17(8):e10239 Drug Test Anal, 2020, 10.1002/dta.2917
S5564	Xylazine	Xylazine is a partial alpha-2 adrenergic agonist that is used for sedation, anesthesia, muscle relaxation, and analgesia in animals such as horses, cattle and other non-human mammals.	Cell Death Dis, 2023, 14(5):318 Cell Death Differ, 2020, 10.1038 Mol Med Rep, 2017, 16(2):1911-1919
S5683	Isoproterenol sulfate dihydrate	Isoproterenol Sulfate is the sulfate salt form of isoproterenol, a beta-adrenergic receptor agonist with bronchodilator activity.	Stem Cell Res Ther, 2022, 13(1):287 Cell Biol Toxicol, 2021, 10.1007/s10565-021-09615-y Biochim Biophys Acta Mol Cell Res, 2021, 1868(10):119080
S4650	Atipamezole	Atipamezole (MPV-1248, MPV1248, Antisedan) is a synthetic α2 adrenergic receptor antagonist. It has also been researched in humans as a potential anti-Parkinsonian drug.	Exp Mol Med, 2020, 10.1038/s12276-020-0461-6 Nitric Oxide, 2019, 85:1-9 Front Neurol, 2019, 10:1041
S4065	Guanabenz Acetate	Guanabenz Acetate (WY-8678) is an selective agonist of α2a-adrenergic receptor, α2b-adrenergic receptor and α2c-adrenergic receptor with pEC50 of 8.25, 7.01 and ~5, respectively.	Cell Stem Cell, 2020, 27(6):876-889.e12 Thyroid, 2019, 29(6):809-823
S3061	Epinephrine HCl	Epinephrine HCl (Adrenaline) is a hormone and a neurotransmitter.	Cell Rep Methods, 2023, 3(10):100599 J Immunother Cancer, 2021, 9(1)e001466
S4296	Salmeterol Xinafoate	Salmeterol Xinafoate(GR 33343X xinafoate,Salmetedur) is a long-acting β2-adrenergic receptor agonist with anti-inflammatory effects, used in the treatment of asthma symptoms and chronic obstructive pulmonary disease (COPD) symptoms.	ACS Pharmacol Transl Sci, 2019, 2(3):148-154 Commun Biol, 2018, 1:106
S3960	Higenamine hydrochloride	Higenamine (Norcoclaurine, (+-)-Demethylcoclaurine), also known as Norcoclaurine HCl, is a non-selective β2 adrenoceptor agonist which is a chemical compound naturally occurring in a number of plants.	Mol Cell Biochem, 2021, 10.1007/s11010-021-04197-z Oncol Rep, 2021, 46(3)202
S4127	Terbutaline Sulfate	Terbutaline Sulfate(Terbutaline hemisulfate) is a selective β2-adrenergic receptor agonist with IC50 of 53 nM.	BMC Pharmacol Toxicol, 2020, 21(1):61 Hum Reprod, 2016, 31(11):2506-2519
S5703	Carvedilol Phosphate	Carvedilol Phosphate is the phosphate salt form of carvedilol, a racemic mixture and adrenergic blocking agent with antihypertensive activity and devoid of intrinsic sympathomimetic activity.	Res Pharm Sci, 2016, 11(5):419-427 Res Pharm Sci, 2015, 10(5):388-96
S3727	Vilanterol Trifenate	Vilanterol trifenatate (GW642444M) is a novel inhaled long-acting beta2 adrenoceptor agonist with inherent 24-hour activity for once daily treatment of COPD and asthma.	Toxicol In Vitro, 2021, 77:105251 J Neuroimmunol, 2019, 332:37-48
S5654	Indacaterol	Indacaterol is an ultra-long-acting β-adrenoceptor agonist with pKi of 7.36 for β1-adrenoceptor and pKi of 5.48 for β2-adrenoceptor.	Drug Test Anal, 2020, 10.1002/dta.2917 J Neuroimmunol, 2019, 332:37-48
S4358	Pimozide	Pimozide (Orap, R6238) is an antagonist of Dopamine Receptors with Ki of 0.83 nM, 3.0 nM and 6600 nM for dopamine D3, D2 and D1 receptors, respectively. Pimozide also exhibits binding affinity at 5-HT1A and α1-adrenoceptor with Ki of 310 nM and 39 nM, respectively. Pimozide is an antipsychotic drug with anti-tumor activity and suppresses STAT3 and STAT5 activity.	Cell Rep Med, 2023, 10.1016/j.xcrm.2023.101286 Biol Pharm Bull, 2021, 10.1248/bpb.b21-00531
S2086	Ivabradine HCl	Ivabradine HCl (S 16257-2,S-18982 D6 hydrochloride), a new I_f inhibitor with IC 50 of 2.9 μM which acts specifically on the pacemaker activity of the sinoatrial node, is a pure heart rate lowering agent.	Cell Rep, 2022, 38(10):110468 J Pain, 2018, 19(6):626-634
S2091	Betaxolol	Betaxolol (SL 75212,Dextrobetaxolol) is a selective beta1 adrenergic receptor blocker used in the treatment of hypertension and glaucoma.	Nat Commun, 2020, 24;11(1):1990 Chirality, 2018, 30(11):1195-1205
S5430	Metoprolol	Metoprolol is a cardioselective β1-adrenergic blocking agent with log Kd values of −7.26±0.07, −6.89±0.09, −5.16±0.12 for β1, β2, and β3 adrenoceptors, respectively. It is used for acute myocardial infarction, heart failure, angina pectoris and mild to moderate hypertension.	BMC Pharmacol Toxicol, 2024, 25(1):25 BMC Pharmacol Toxicol, 2024, 25(1):25 Cell Rep, 2022, 38(10):110468
S4817	Atenolol	Atenolol (Tenormin, Normiten, Blokium) is a selective β1 receptor antagonist with log Kd values of −6.66±0.05, −5.99±0.14, −4.11±0.07 for binding to the human β1-, β2- and β3-adrenoceptors.	Int J Mol Sci, 2022, 23(21)12948 Oncol Rep, 2021, 46(3)202
S5494	Salbutamol	Salbutamol (Albuterol) is a short-acting, selective beta2-adrenergic receptor agonist used to treat or prevent bronchospasm in patients with asthma, bronchitis, emphysema, and other lung diseases.	Front Physiol, 2022, 13:800055 BMC Pharmacol Toxicol, 2020, 21(1):61
S1409	Alfuzosin HCl	Alfuzosin HCI(SL 77499 HCl) is an alpha1 receptor antagonist used to treat benign prostatic hyperplasia (BPH).	J Immunother Cancer, 2024, 12(11)e009805 Prostate, 2016, 76(8):757-66
S3083	Indacaterol Maleate	Indacaterol (QAB149) is an ultra-long-acting β-adrenoceptor agonist with pK_i of 7.36 for β1-adrenoceptor and pK_i of 5.48 for β2-adrenoceptor.	J Allergy Clin Immunol, 2021, S0091-6749(21)00979-9
S2458	Clonidine HCl	Clonidine HCl(Kapvay) is a direct-acting α2 adrenergic agonist with an ED50 of 0.02±0.01 mg/kg.	J Immunother Cancer, 2024, 12(11)e009805 Mol Pain, 2022, 18:17448069221107810
S1424	Prazosin HCl	Prazosin HCl (cp-12299-1) is a competitive alpha-1 adrenoceptor antagonist, used to treat high blood pressure or benign prostatic hyperplasia.	J Immunother Cancer, 2024, 12(11)e009805 BMC Pharmacol Toxicol, 2020, 21(1):61
S2038	Phentolamine Mesylate	Phentolamine Mesylate(Phentolamine methanesulfonate) is a reversible and nonselective alpha-adrenergic receptor antagonist, used for the prevention or control of hypertensive episodes.	J Immunother Cancer, 2024, 12(11)e009805 Int J Mol Sci, 2024, 25(18)10162 Sci Rep, 2024, 14(1):4178
S2059	Terazosin HCl Dihydrate	Terazosin HCl is a selective α1-adrenoceptor antagonist, used for treatment of symptoms of an enlarged prostate (BPH).	J Biomed Sci, 2021, 28(1):8
S2517	Maprotiline HCl	Maprotiline HCl is a selective noradrenalin re-uptake inhibitor, used in the treatment of depression.	Front Pharmacol, 2021, 12:689767
S4113	Desvenlafaxine	Desvenlafaxine (WY 45233 Succinate) is a serotonin (5-HT) and norepinephrine (NE) reuptake inhibitor with K_i of 40.2 nM and 558.4 nM, respectively.	Am J Cancer Res, 2024, 14(3):1087-1100 Drug Metab Dispos, 2020, 48(10):1044-1052
S2126	Naftopidil	Naftopidil (KT-611) is a selective α1-adrenergic receptor antagonist with K_i of 3.7 nM, 20 nM, and 1.2 nM for α1a, α1b, and α1d, respectively, used for the treatment of benign prostatic hyperplasia.	Cell Syst, 2019, 8(2):97-108
S4123	Timolol Maleate	Timolol Maleate (MK-950,(S)-Timolol Maleate) is a non-selective, beta-adrenergic receptor antagonist for β1/β2 with K_i of 1.97 nM/2.0 nM.	J Immunother Cancer, 2024, 12(11)e009805 J Dermatolog Treat, 2020, 24:1-7
S4010	Acebutolol HCl	Acebutolol is a β-adrenergic receptors antagonist used in the treatment of hypertension, angina pectoris and cardiac arrhythmias.	Front Pharmacol, 2021, 12:740529
S3060	Medetomidine HCl	Medetomidine is a selective α2-adrenoceptor agonist, with K_i of 1.08 nM, exhibts 1620-fold selectivity over α1-adrenoceptor.	Micromachines, 2018, 9(6)
S1437	Tizanidine HCl	Tizanidine HCl (DS 103-282) is an α2-adrenergic receptor agonist and inhibits neurotransmitter release from CNS noradrenergic neurons.	Drug Metab Dispos, 2021, 49(8):638-647
S1827	Betaxolol HCl	Betaxolol (SL 75212) is a β₁ adrenergic receptor blocker with IC50 of 6 μM.	J Immunother Cancer, 2024, 12(11)e009805 Chirality, 2018, 30(11):1195-1205
S2092	Detomidine HCl	Detomidine HCl(MPV 253AII) produce dose-dependent sedative and analgesic effects, mediatated by activation of α2 catecholamine receptors.	J Immunother Cancer, 2024, 12(11)e009805 Nature, 2018, 560(7718):372-376
S5537	Tizanidine	Tizanidine is an imidazoline derivative and a centrally acting α2 adrenergic agonist used as a muscle relaxant for therapy of acute muscle spasms and chronic spasticity.	Drug Metab Dispos, 2021, 49(8):638-647
S5768	Fenoterol hydrobromide	Fenoterol hydrobromide (Phenoterol) is the the hydrobromide salt of fenoterol, a β2 adrenoreceptor agonist with bronchodilator activity.	Toxicol In Vitro, 2021, 77:105251
S4124	Tolazoline HCl	Tolazoline(Imidaline hydrochloride,NSC35110 hydrochloride) is a non-selective competitive α-adrenergic receptor antagonist.	J Immunother Cancer, 2024, 12(11)e009805 Insect Biochem Mol Biol, 2017, 90:61-70
S5942	Bisoprolol	Bisoprolol is a cardioselective β1-adrenergic blocking agent used for secondary prevention of myocardial infarction (MI), heart failure, angina pectoris and mild to moderate hypertension.	J Pathol, 2022, 10.1002/path.6020
S5337	Rauwolscine hydrochloride	Rauwolscine hydrochloride (Isoyohimbine, α-Yohimbine, corynanthidine) is the hydrochloride salt form of Rauwolscine, a specific and potent α2 antagonist with Ki of 12 nM.	J Pharm Biomed Anal, 2020, 180:113019
S3656	Piribedil	Piribedil (Trivastal, Trivastan) is a relatively selective dopamine (D2/D3) agonist with moderate antidepressant activity. It also has α2-adrenergic (α2A/α2C) antagonist properties.	Cell Rep Methods, 2023, 3(1):100381 Cell Rep Methods, 2023, 3(1):100381
E2901	(-)-Isoproterenol hydrochloride	(-)-Isoproterenol hydrochloride is an agonist of beta-adrenergic receptor. (-)-Isoproterenol hydrochloride is also used in the treatment of bradycardia; bronchodilator.	Stem Cell Res Ther, 2022, 13(1):287
S4679	Terazosin HCl	Terazosin (Hytrin, Zayasel, Terazosine, Flumarc, Fosfomic, Blavin) is a selective alpha-1 antagonist used for treatment of symptoms of an enlarged prostate (BPH). It works by blocking the action of adrenaline on smooth muscle of the bladder and the blood vessel walls.	J Immunother Cancer, 2024, 12(11)e009805 J Biomed Sci, 2021, 28(1):8
S5780	Prazosin	Prazosin is an α1-blocker that acts as an inverse agonist at alpha-1 adrenergic receptors. It is used to treat hypertension.	BMC Pharmacol Toxicol, 2020, 21(1):61
S5787	Dronedarone	Dronedarone (SR33589) is a derivative of amiodarone which is classified as a Class III antiarrhythmic agent. It shows rate-dependent inhibition of the rapid Na+ current, inhibits α and β-adrenergic receptors like Class II agents, exhibits blockade of K+ outward currents as the main mechanism of action of Class III, and effectively block slow Ca2+ inward currents (Class IV).	Korean Circ J, 2024, 54(4):172-186 Chem Res Toxicol, 2021, 10.1021/acs.chemrestox.1c00127
S4112	Desvenlafaxine Succinate hydrate	Desvenlafaxine Succinate hydrate (WY 45233) is a new serotonin (5-HT) transporter and norepinephrine (NE) transporter reuptake inhibitor with K_i of 40.2 nM and 558.4 nM respectively.	Drug Metab Dispos, 2020, 48(10):1044-1052
S5023	Nadolol	Nadolol (Corgard, Solgol, Anabet, SQ11725) is a non-selective beta-adrenergic antagonist with antihypertensive and antiarrhythmic activities.	J Chromatogr A, 2024, 1734:465286 Eur J Drug Metab Pharmacokinet, 2022, 10.1007/s13318-022-00780-x
S4243	Deoxycorticosterone acetate	Deoxycorticosterone acetate (11-Deoxycorticosterone, DOC, Cortexone) is a steroid hormone used for intramuscular injection for replacement therapy of the adrenocortical steroid.	Nat Cancer, 2020, 1(2):235-248
S2113	Cisatracurium Besylate	Cisatracurium Besylate(51W89) is a nondepolarizing neuromuscular blocking agent, antagonizing the action of acetylcholine by inhibiting neuromuscular transmission.	Biosci Trends, 2021, 15(1):50-54
S2020	Formoterol Hemifumarate	Formoterol Hemifumarate (Eformoterol, CGP 25827A, NSC 299587, YM 08316,Formoterol fumarate) is a potent, selective and long-acting β2-adrenoceptor agonist used in the management of asthma and chronic obstructive pulmonary disease(COPD).
S1613	Silodosin	Silodosin (KAD 3213, KMD 3213) is a highly selective α1A-adrenoceptor antagonist, used in treatment of benign prostatic hyperplasia.	J Immunother Cancer, 2024, 12(11)e009805
S2691	BMY 7378 Dihydrochloride	BMY 7378 is a multi-targeted inhibitor of α2C-adrenoceptor and α1D-adrenoceptor with pK_i of 6.54 and 8.2, respectively, and acts as a mixed agonist and antagonist for 5-HT1A receptor with pK_i of 8.3.
S3041	Droxidopa	Droxidopa (L-DOPS) is a psychoactive drug and acts as a prodrug to the neurotransmitters norepinephrine (noradrenaline) and epinephrine (adrenaline).	bioRxiv, 2024, 2024.07.30.605812
S2522	L-Adrenaline	L-Adrenaline (Epinephrine) belongs to a group of the compounds known as catecholamines.This product is a hazardous chemical (acute toxicity/flammable/skin corrosive). Please use it while wearing a protective face mask, gloves, and clothing.	J Immunother Cancer, 2024, 12(11)e009805
S1856	Metoprolol Tartrate	Metoprolol Tartrate (CGP 2175E) is a selective β1 receptor blocker medication, used to treat hypertension and heart failure.	J Immunother Cancer, 2024, 12(11)e009805
S1387	Naftopidil DiHCl	Naftopidil DiHCl (Flivas, KT-611, Avishot,BM-15275) is a selective 5-HT1A and α1-adrenergic receptor antagonist with IC50 of 0.1 μM and 0.2 μM, respectively.
S2499	Phenoxybenzamine HCl	Phenoxybenzamine HCl (NSC 37448, NCI-c01661) is a non-specific, irreversible alpha antagonist with an IC50 of 550 nM.
S2519	Naphazoline HCl	Naphazoline HCl is an ocular vasoconstrictor and imidazoline derivative sympathomimetic amine.
S2533	Ritodrine HCl	Ritodrine HCl (NSC 291565,DU 21220, Ritodrine) is a hydrochloride salt of ritodrine which is a β-2 adrenergic receptor agonist.
S2438	Synephrine HCl	SynephrineHCl (Oxedrine, p-Synephrine) is a sympathomimetic α-adrenergic receptor (AR) agonist.
S3153	Levalbuterol tartrate	Levalbuterol tartrate(Levosalbutamol tartrate) is a relatively selective beta2-adrenergic receptor agonist used for the treatment of asthma.	J Immunother Cancer, 2024, 12(11)e009805
S3294	Demethyl-Coclaurine	Demethyl-Coclaurine (Higenamine, Norcoclaurine), the key component of the Chinese herb aconite root, is a beta-2 adrenergic receptor (β2-AR) agonist. Demethyl-Coclaurine stimulates AKT phosphorylation and requires PI3K activation for the anti-apoptotic effect in cardiomyocytes.	Signal Transduct Target Ther, 2024, 9(1):243
S2545	Scopine	Scopine(6,7-Epoxytropine) is the metabolite of anisodine, which is a α1-adrenergic receptor agonist and used in the treatment of acute circulatory shock.
S2607	Buflomedil HCl	Buflomedil HCl(NSC 759291) is a vasodilator used to treat claudication or the symptoms of peripheral arterial disease; A nonselective alpha adrenergic receptor inhibitor.	J Immunother Cancer, 2024, 12(11)e009805
S5088	Labetalone hydrochloride	Labetalone hydrochloride (Benzoic amide) is hydrochloride form of labetalone, a blocker of both alpha- and beta-adrenergic receptors that is used as an antihypertensive.
S2523	DL-Adrenaline	DL-Adrenaline(dl-Epinephrine) is a hormone and a neurotransmitter secreted by the medulla of the adrenal glands.
S4266	Brimonidine Tartrate	Brimonidine Tartrate(UK 1434 Tartrate) is a highly selective α-adrenergic receptor agonist with EC50 of 0.45 nM for the α2A adrenoreceptor, and used to treat open-angle glaucoma or ocular hypertension.
S5540	Landiolol hydrochloride	Landiolol hydrochloride (ONO-1101) is the hydrochloride salt form of Landiolol, which is an ultra-short-acting β1 selective adrenoceptor antagonist.
S2615	Noradrenaline bitartrate monohydrate	Noradrenaline bitartrate monohydrate (Levophed) is a direct alpha-adrenergic receptors stimulator.
S0032	Batefenterol	Batefenterol (GSK961081, TD-5959) is both a muscarinic receptor antagonist and a β2-adrenoceptor agonist with Ki of 1.4 nM, 1.3 nM and 3.7 nM for hM2, hM3 muscarinic receptors and hβ2-adrenoceptor, respectively.
E4888^New	Guanabenz hydrochloride	Guanabenz hydrochloride(NE56490) is a small molecule, antihypertensive agonist of α2-adrenoceptor. It also inhibits eIF2α and GADD34, showing potential for treating cardiac hypertrophy, heart failure, atherosclerosis, and ischemic heart disease.
E4825^New	Naphazoline (nitrate)	Naphazoline (nitrate) is a agonist of peripheral α2-adrenergic receptor and used as a topical decongestant. It also acts as a vasoconstrictor that effectively reduces intraoperative bleeding and enhances postoperative analgesia. When used in conjunction with intranasal lidocaine, it significantly reduces both intra- and postoperative pain, thereby decreasing the need for rescue analgesics in the postoperative period following septorhinoplasty.
S5802	Alprenolol hydrochloride	Alprenolol hydrochloride is the hydrochloride salt form of alprenolol, which is an beta adrenergic receptorantagonist and is used as an antihypertensive, anti-anginal, and anti-arrhythmic agent.
S5769	Fenoterol	Fenoterol (Phenoterol) is a β2 adrenoreceptor agonist with bronchodilator activity.
S7538	RS-102895 Hydrochloride	RS-102895 hydrochloride (HCl) is a potent antagonist of Chemokine (C-C motif) receptor 2 (CCR2) with IC50 of 360 nM, and shows no effect on CCR1. RS-102895 hydrochloride also inhibits human α1a and α1d receptors, rat brain cortex 5-HT1a receptor in cells with IC50s of 130 nM, 320 nM, 470 nM, respectively.
S4135	Clorprenaline HCl	Clorprenaline HCl (NSC 334693) is a β2-receptor agonist, it has a significant expansion of the bronchial effect.
S5666	Moxisylyte hydrochloride	Moxisylyte hydrochloride (thymoxamine) is an alpha-adrenergic blocking agent used for the treatment of Raynaud's disease.	J Immunother Cancer, 2024, 12(11)e009805
S6345	3-Nitro-L-tyrosine	3-Nitro-L-tyrosine (3-NT, N-Tyr, MNT), synthesized from L-tyrosine by peroxynitrite, is a product of nitric oxide and superoxide. 3-Nitro-L-tyrosine inhibits the hemodynamic responses to angiotensin II, possibly through the inhibition of alpha 1-adrenoceptor-mediated events.
S5766	Alfuzosin	Alfuzosin(SL 77499), a quinazoline derivative, is a selective and competitive α1-adrenoceptor antagonist.
S4043	Tetrahydrozoline HCl	Tetrahydrozoline (Tetryzoline) HCl is an imidazoline derivative with alpha receptor agonist activity.
S0862	L-765314	L-765314 is a selective and potent α1b-adrenoceptor (α1b adrenergic receptor) antagonist with an IC50 of 1.90 nM and Kis of 5.4 and 2.0 for rat and human α1b adrenergic receptor, respectively.
E4865^New	Noradrenaline bitartrate	Noradrenaline bitartrate (Norepinephrine Bitartrate) is a central nervous system (CNS) neurotransmitter and stimulator of β1 adrenergic receptors and α-adrenergic receptors, causing increased contractility and heart rate, as well as vasoconstriction.
E2875^New	Levobunolol(l-Bunolol) hydrochloride	Levobunolol (l-Bunolol) hydrochloride is a potent and nonselective β-adrenergic receptor antagonist with an IC50 of 48 μM.
S9285	Fargesin	Fargesin is a neolignan isolated from Magnolia plants. It is a potential β1AR antagonist through cAMP/PKA pathway.
S5789	Propafenone	Propafenone (SA-79) is an orally active sodium channel blocking agent and a beta-adrenoceptor (β-adrenergic receptor) antagonist. Propafenone offers a broad spectrum of activity in the treatment of cardiac arrhythmias.
S5965	Urapidil	Urapidil is an antihypertensive drug acting as an α1 adrenoreceptor antagonist and a 5-HT1A agonist.
E4963^New	Clonidine	Clonidine(Clonidin) is a direct-acting α2-adrenergic agonist. It is potentially used in the treatment of attention-deficit hyperactivity disorder (ADHD) in children and adolescents.
S5217	Arformoterol Tartrate	Arformoterol Tartrate is the tartrate salt of arformoterol, a long-acting beta-2 adrenergic agonist with bronchodilator activity.
S5281	Dapiprazole Hydrochloride	Dapiprazole Hydrochloride (Glamidolo Hydrochloride, Reversil Hydrochloride) is the hydrochloride salt form of dapiprazole, an alpha-adrenergic blocker used to reverse mydriasis after eye examination.
S5734	Midodrine hydrochloride	Midodrine hydrochloride is the hydrochloride salt form of midodrine, an adrenergic alpha-1 agonist used as a vasopressor.
S5735	Midodrine	Midodrine belongs to the class of medications known as vasopressors. It is an adrenergic alpha-1 agonist.
S9470	Penbutolol Sulfate	Penbutolol sulfate ((-)-Terbuclomine) is an effective beta-adrenergic receptor blocker and diuretic that is used as an antihypertensive agent.
S5727	Tetryzoline	Tetryzoline (Tetrahydrozoline) is an alpha-adrenergic agonist used in some over-the-counter eye drops and nasal sprays.
S5954	L-(-)-α-Methyldopa hydrate	L-(-)-α-Methyldopa (Methyldopa, MK-351) hydrate, a potent antihypertensive drug, is a selective agonist for α2-adrenergic receptors.
S1642	Methyldopa	Methyldopa (Aldomet) is a DOPA decarboxylase competitive inhibitor with an ED50 of 21.8 mg/kg.	J Immunother Cancer, 2024, 12(11)e009805
E4842^New	Vilanterol	Vilanterol (GW642444) is a potent and selective agonist of β2-adrenoceptor (β2-AR) with pEC50 of β2-AR, β1-AR, and β3-AR is 10.37, 6.98 and 7.36 respectively in cAMP detection assays.
S2576	Xylometazoline HCl	Xylometazoline is an α-adrenoceptor agonist commonly used as nasal decongestant, exhibits highest potency at α_2B-adrenoceptor subtype with EC50 of 99 μM.
S3913	Pimethixene maleate	Pimethixene (Pimetixene) maleate, an antihistamine, anntimigraine agent and antiserotonergic compound, is a highly potent antagonist of a broad range of monoamine receptors, including a variety of serotonin receptors. Pimethixene maleate inhibits 5-HT2A, 5-HT2B, 5-HT2C, 5-HT1A, 5-HT1B, 5-HT6, 5-HT7, Adrenergic α-1A, Dopamine D1 Receptor, Dopamine D2 Receptor, Dopamine D4.4 Receptor, Histamine H1 Receptor, Muscarinic M1 and Muscarinic M2 with pKi of 10.22, 10.44, 8.42, 7.63, < 5, 7.30, 7.28, 7.61, 6.37, 8.19, 7.54, 10.14, 8.61 and 9.38, respectively.
S3640	Methoxyphenamine Hydrochloride	Methoxyphenamine Hydrochloride (2-methoxy-N-methylamphetamine, OMMA) is a β-adrenergic receptor agonist of the amphetamine class used as a bronchodilator.
S4649	Atipamezole hydrochloride	Atipamezole (Antisedan, MPV1248) is a synthetic α2 adrenergic receptor antagonist. It has also been researched in humans as a potential anti-Parkinsonian drug. Atipamezole hydrochloride is hydrochloride form of atipamezole.
S2304	Gramine	Gramine (Donaxine) is a natural indole alkaloid isolated from giant reed, acts as an active adiponectin receptor (AdipoR) agonist, with IC50 of 3.2 µM and 4.2 µM for AdipoR2 and AdipoR1, respectively. Gramine is also a human and mouse β2-Adrenergic receptor (β2-AR) agonist.
S0116	Piperoxan hydrochloride	Piperoxan hydrochloride (Benodaine, Fourneau 933, F933, DL-Piperoxan) is an antagonist of α2 (alpha 2) adrenoceptor.
S5981	S(-)-Propranolol hydrochloride	(S)-(-)-Propranolol hydrochloride, the active enantiomer of propranolol, is a β-Adrenoceptor (β-Adrenergic Receptor) antagonist with log Kd values of -8.16, -9.08, and -6.93 for β1, β2, and β3, respectively.	Heliyon, 2024, 10(11):e31865
S0812	SR59230A	SR59230A is a blood-brain barrier penetrating, potent and selective antagonist of β3-adrenergic receptor with IC50 of 40 nM, 408 nM, and 648 nM for β3, β1, and β2 receptors, respectively.
S1423	Dobutamine HCl	Dobutamine(Dobutrex) hydrochloride is a selective potent agonist of β1-AR (β-1 adrenergic receptor) and exhibits weak activity at α1-AR and β2-AR. Dobutamine is a sympathomimetic compound that effectively restores blood pressure in hypotensive dogs and human patients by improving myocardial contractility and increasing cardiac output (CO).
S6583	Apraclonidine HCl	Apraclonidine (Iopidine,ALO 2145) is a sympathomimetic used in glaucoma therapy. It is an alpha2-adrenergic agonist.
S3764	Isoferulic Acid	Isoferulic acid (Hesperetic acid, Hesperetate, Isoferulate), a major active ingredient of Cimicifuga heracleifolia, shows anti-inflammatory, antiviral, antioxidant, and antidiabetic properties. Isoferulic acid (3-Hydroxy-4-methoxycinnamic acid) is a cinnamic acid derivative that has antidiabetic activity. Isoferulic acid binds to and activates α1-adrenergic receptors (IC50=1.4 µM) to enhance secretion of β-endorphin (EC50=52.2 nM) and increase glucose use.
S4485	Olodaterol	Olodaterol is a long-acting β2-adrenergic receptor agonist that is used as a component of an inhalation (Tiotropium/Olodaterol) for treating patients with chronic obstructive pulmonary disease (COPD).
S9050	Boldine	Boldine, isolated from Peumus boldus, has alpha-adrenergic antagonist activities in vascular tissue with anti-oxidant, hepatoprotective, cytoprotective, antipyretic and anti-inflammatory effects.
S4693	Guanfacine Hydrochloride	Guanfacine Hydrochloride (Tenex, Intuniv) is a selective α2A-adrenoceptor agonist with anti-hypertensive effect.	J Immunother Cancer, 2024, 12(11)e009805
S1435	Tamsulosin hydrochloride	Tamsulosin (Flomax) hydrochloride is an antagonist of alpha1A adrenoceptors in the prostate.
S5669	Isoxsuprine hydrochloride	Isoxsuprine hydrochloride is a beta-adrenergic agonist with vasodilator activity.
S4085	Levobetaxolol HCl	Levobetaxolol (AL 1577A,(S)-Betaxolol hydrochloride) exhibits a higher affinity at cloned human β1 and β2 receptors with K_i value of 0.76 nM and 32.6 nM, respectively.	J Immunother Cancer, 2024, 12(11)e009805
S5042	Bevantolol hydrochloride	Bevantolol hydrochloride (NC-1400) is a cardioselective, beta adrenoceptor antagonist, devoid of intrinsic β sympathomimetic activity and with weak membrane-stabilizing and local anesthetic properties.
S5925	Olodaterol hydrochloride	Olodaterol hydrochloride (BI-1744) is the hydrochloride salt form of Olodaterol, which is a long-acting beta2-adrenergic agonist.
E0949	Mebicar	Mebicar, a derivative of bicyclic bis-ureas, inhibits the orientation reaction in albino mice, potentiates the action of narcotic hypnotics, abolishes the conditioned reflex reaction of avoidance, displays central adrenolytic activity, interferes with the norepinephrine metabolism in the brain stem.
E1049^New	CL316243	CL316243 is a highly potent and selective agonist of β3-adrenoceptor with an EC50 value of 3 nM, respectively but is an extremely poor to β1/2- receptors.It effectively stimulates adipocyte lipolysis and increases brown adipose tissue thermogenesis and metabolic rate.
S5778	Esmolol	Esmolol is a cardioselective beta1 receptor blocker with rapid onset, a very short duration of action, and no significant intrinsic sympathomimetic or membrane stabilising activity at therapeutic dosages.
S6407	Tulobuterol hydrochloride	Tulobuterol is a long-acting β2-adrenergic receptor agonist that has bronchodilatory, anti-inflammatory, and antiviral activities.
E0408	JP1302	JP-1302(MMV006172), a novel highly selective α_2C-adrenoceptor antagonist with Kb of 16 nM at the α_2C-adrenoceptor subtype, also produces antidepressant and antipsychotic-like effects.
E4880^New	Labetalol	Labetalol (AH5158, Sch-15719W free base) is an orally active and selective competitive antagonist of α1-adrenergic receptors and non-selective β-adrenergic receptors. Labetalol, an anti-hypertensive agent is used in the research of cardiovascular diseases.
S4100	Esmolol HCl	Esmolol (ASL8052) is a cardioselective b-blocker, used to control rapid heartbeats or abnormal heart rhythms.	J Immunother Cancer, 2024, 12(11)e009805
S5496	Guanethidine Monosulfate	Guanethidine monosulfate is an antihypertensive agent that acts by inhibiting selectively transmission in post-ganglionic adrenergic nerves.
S5782	Doxazosin	Doxazosin(UK 33274) is a quinazoline-derivative that selectively antagonizes postsynaptic α1-adrenergic receptors.
E4892^New	Formoterol	Formoterol is a highly selective and potent long-acting beta2-adrenergic agonist that functions by binding to and activating beta2-adrenergic receptors on the smooth muscle cells of the airways. It is used in the treatment of patients with chronic obstructive pulmonary disease (COPD).
S2174	Hydroxyflutamide (Hydroxyniphtholide)	Hydroxyflutamide (SCH-16423, Hydroxyniphtholide) is an androgen receptor (AR) antagonist and possesses an IC50 of 0.7 μM for the androgen receptor.
S5923	Celiprolol hydrochloride	Celiprolol is a β1-adrenoceptor antagonist with partial β2 agonist activity.
S6447	Carazolol	Carazolol is a non-specific β-adrenergic receptor blocking agent and binds to β receptors irreversibly.
E2944	Norepinephrine hydrochloride	Norepinephrine (Levarterenol; L-Noradrenaline) hydrochloride is a potent agonist of adrenergic receptor (AR). Norepinephrine activates α1, α2, β1 receptors.
E4849^New	Terbutaline	Terbutaline(Brican, Brethine), an active metabolite of bambuterol is an orally active agonist of β2-adrenergic receptor, that increases MKP-1 expression. Terbutaline is used in the treatment of obstructive lung diseases as a bronchodilator remedy. It also exhibits anti-inflammatory effects.
S5341	Metroprolol succinate	Metroprolol Succinate (Metoprolol succinate) is the succinate salt form of metoprolol, a cardioselective competitive beta-1 adrenergic receptor antagonist with antihypertensive properties and devoid of intrinsic sympathomimetic activity.
S2083	Procaterol HCl	Procaterol HCl (OPC-2009) is a short-acting β2-adrenergic receptor agonist with K_p of 8 nM, used for the treatment of asthma
S5432	Dibenamine Hydrochloride	Dibenamine (N-(2-Chloroethyl)dibenzylamine, Sympatholytin, Dibenzylchlorethamine) is an irreversible blocker of α1 adrenoceptors.
E2964	Norepinephrine tartrate	Norepinephrine tartrate is a potent agonist of adrenergic receptor (AR). Norepinephrine activates α1, α2, β1 receptors.
S4277	Bambuterol HCl	Bambuterol HCl(Bambuterol hydrochloride,KWD-2183 hydrochloride) is a potent β-adrenoceptor agonist, used in the treatment of asthma.
S4278	Carteolol HCl	Carteolol HCl(Carteolol hydrochloride,OPC-1085 hydrochloride) is a β-adrenoceptor antagonist, used for the treatment of glaucoma.	J Immunother Cancer, 2024, 12(11)e009805
E1746^New	Protokylol hydrochloride	Protokylol hydrochloride(Caytine hydrochloride, JB-251 hydrochloride) is a salt form of protokylol and is an agonist of β-adrenergic receptor. Protokylol hydrochloride is also used as a bronchodilator.
S5750	DL-Norepinephrine hydrochloride	Norepinephrine (noradrenaline) is the neurotransmitter at most sympathetic neuroeffector junctions and has pharmacologic effects on both α1 and β1 adrenoceptors.
S9560	Anisodamine Hydrobromide	Anisodamine (6-Hydroxyhyoscyamine) is a naturally occurring atropine derivative and exhibits anti-inflammatory activity. It also inhibits α1-adrenergic receptors and muscarinic acetylcholine receptors (mAChRs).
S2362	Synephrine	Synephrine (Oxedrine), a natural protoalkaloid in the extract of bitter orange and other citrus species, is commonly used for weight loss.
S9508	Brimonidine	Brimonidine (Bromoxidine, UK 1430) is an alpha adrenergic receptor agonist (primarily alpha-2) and is used for the treatment of open-angle glaucoma or ocular hypertension to lower intraocular pressure.
E0529	Metipranolol	Metipranolol (Betamann) is a potent β-adrenergic receptor antagonist, possessing the beta-blocking potencies (pA2) of 8.3, 8.4 at guinea pig atrial β1-adrenoceptor and β2-adrenoceptor of the rat uterus, respectively, also is a potent displacer of ³H-DHA binding, ligand concentration 0.7 nM, possessing a Ki value of 39 ± 24 nM.
S0896	DSP-4 HCl	DSP-4 hydrochloride (Neurotoxin DSP 4 (hydrochloride)) can be used for the temporary selective degradation of the central and peripheral noradrenergic neurons, which exclusively affects the noradrenergic fibers from the LC (locus coeruleus).
E0785	YS-49	YS-49 is a PI3K/Akt (a downstream target of RhoA) activator, to reduce RhoA/PTEN activation in the 3-methylcholanthrene-treated cells, inhibits angiotensin II (Ang II)-stimulated proliferation of VSMCs via induction of heme oxygenase (HO)-1, also is an isoquinoline compound alkaloid, has a strong positive inotropic action through activation of cardiac β-adrenoceptors.	Signal Transduct Target Ther, 2024, 9(1):243
S4291	Labetalol HCl	Labetalol HCl(AH-5158 hydrochloride,Labetalol hydrochloride,Sch-15719W) is a dual antagonist for both selective alpha1-adrenergic and nonselective beta-adrenergic receptors, used in the treatment of high blood pressure.	J Immunother Cancer, 2024, 12(11)e009805
S5267	Nylidrin Hydrochloride	Nylidrin Hydrochloride (Buphenine), a β-adrenergic agonist, is used therapeutically for its vasodilating effect on the peripheral circulation and possibly on the cerebral circulation as well.
S5723	Carvedilol EP IMpurity E	Carvedilol is a nonselective beta blocker/alpha-1 blocker and used in management of congestive heart failure (CHF).
S6487	fluticasone furoate	Fluticasone furoate (GW685698) is an inhaled corticosteroid/long-acting beta-agonist combination with a prolonged bronchodilator duration of action. It is used for the treatment of non-allergic and allergic rhinitis administered by a nasal spray.
S3185	Adrenalone HCl	Adrenalone is an adrenergic agonist used as a topical vasoconstrictor and hemostatic, mainly acts on alpha-1 adrenergic receptors.	J Immunother Cancer, 2024, 12(11)e009805
S4481	Guanabenz	Guanabenz (GBZ, GA, Wytensin, Wy-8678,BR-750) is an orally active central alpha 2-adrenoceptor (α2 adrenergic receptor) agonist with antihypertensive action.
S4797	Nicergoline	Nicergoline is an ergot derivative used to treat senile dementia and other disorders with vascular origins. It has a selective alpha-1A adrenergic receptor blocking property and also other additional mechanisms of actions.
S4076	Propranolol HCl	Propranolol HCl (AY-64043, ICI-45520, NCS-91523) is a competitive non-selective beta-adrenergic receptors inhibitor.	Cell Res, 2024, 10.1038/s41422-024-00946-z J Immunother Cancer, 2024, 12(11)e009805 Sci Rep, 2024, 14(1):4178
S1206	Bisoprolol fumarate	Bisoprolol fumarate (EMD33512) is a selective type β1 adrenergic receptor blocker.	J Immunother Cancer, 2024, 12(11)e009805 J Pathol, 2022, 10.1002/path.6020 Front Nutr, 2022, 9:907986
S1324	Doxazosin Mesylate	Doxazosin, a quinazoline-derivative, selectively antagonizes postsynaptic α1-adrenergic receptors, used in the treatment of high blood pressure and urinary retention associated with benign prostatic hyperplasia.	J Immunother Cancer, 2024, 12(11)e009805 J Exp Clin Cancer Res, 2023, 10.1186/s13046-023-02866-z J Ocul Pharmacol Ther, 2017, 33(1):50-56
S5739	Nebivolol	Nebivolol (Bystolic,R 065824) is a β1 receptor blocker with nitric oxide-potentiating vasodilatory effect used in treatment of hypertension and also for left ventricular failure.	Int J Mol Sci, 2023, 24(11)9708 Front Pharmacol, 2022, 13:1049640 Front Pharmacol, 2021, 12:691998
S5703	Carvedilol Phosphate	Carvedilol Phosphate is the phosphate salt form of carvedilol, a racemic mixture and adrenergic blocking agent with antihypertensive activity and devoid of intrinsic sympathomimetic activity.	Res Pharm Sci, 2016, 11(5):419-427 Res Pharm Sci, 2015, 10(5):388-96
S2086	Ivabradine HCl	Ivabradine HCl (S 16257-2,S-18982 D6 hydrochloride), a new I_f inhibitor with IC 50 of 2.9 μM which acts specifically on the pacemaker activity of the sinoatrial node, is a pure heart rate lowering agent.	Cell Rep, 2022, 38(10):110468 J Pain, 2018, 19(6):626-634
S4113	Desvenlafaxine	Desvenlafaxine (WY 45233 Succinate) is a serotonin (5-HT) and norepinephrine (NE) reuptake inhibitor with K_i of 40.2 nM and 558.4 nM, respectively.	Am J Cancer Res, 2024, 14(3):1087-1100 Drug Metab Dispos, 2020, 48(10):1044-1052
S5787	Dronedarone	Dronedarone (SR33589) is a derivative of amiodarone which is classified as a Class III antiarrhythmic agent. It shows rate-dependent inhibition of the rapid Na+ current, inhibits α and β-adrenergic receptors like Class II agents, exhibits blockade of K+ outward currents as the main mechanism of action of Class III, and effectively block slow Ca2+ inward currents (Class IV).	Korean Circ J, 2024, 54(4):172-186 Chem Res Toxicol, 2021, 10.1021/acs.chemrestox.1c00127
S4112	Desvenlafaxine Succinate hydrate	Desvenlafaxine Succinate hydrate (WY 45233) is a new serotonin (5-HT) transporter and norepinephrine (NE) transporter reuptake inhibitor with K_i of 40.2 nM and 558.4 nM respectively.	Drug Metab Dispos, 2020, 48(10):1044-1052
S2113	Cisatracurium Besylate	Cisatracurium Besylate(51W89) is a nondepolarizing neuromuscular blocking agent, antagonizing the action of acetylcholine by inhibiting neuromuscular transmission.	Biosci Trends, 2021, 15(1):50-54
S5088	Labetalone hydrochloride	Labetalone hydrochloride (Benzoic amide) is hydrochloride form of labetalone, a blocker of both alpha- and beta-adrenergic receptors that is used as an antihypertensive.
S6345	3-Nitro-L-tyrosine	3-Nitro-L-tyrosine (3-NT, N-Tyr, MNT), synthesized from L-tyrosine by peroxynitrite, is a product of nitric oxide and superoxide. 3-Nitro-L-tyrosine inhibits the hemodynamic responses to angiotensin II, possibly through the inhibition of alpha 1-adrenoceptor-mediated events.
S9470	Penbutolol Sulfate	Penbutolol sulfate ((-)-Terbuclomine) is an effective beta-adrenergic receptor blocker and diuretic that is used as an antihypertensive agent.
S1642	Methyldopa	Methyldopa (Aldomet) is a DOPA decarboxylase competitive inhibitor with an ED50 of 21.8 mg/kg.	J Immunother Cancer, 2024, 12(11)e009805
S3913	Pimethixene maleate	Pimethixene (Pimetixene) maleate, an antihistamine, anntimigraine agent and antiserotonergic compound, is a highly potent antagonist of a broad range of monoamine receptors, including a variety of serotonin receptors. Pimethixene maleate inhibits 5-HT2A, 5-HT2B, 5-HT2C, 5-HT1A, 5-HT1B, 5-HT6, 5-HT7, Adrenergic α-1A, Dopamine D1 Receptor, Dopamine D2 Receptor, Dopamine D4.4 Receptor, Histamine H1 Receptor, Muscarinic M1 and Muscarinic M2 with pKi of 10.22, 10.44, 8.42, 7.63, < 5, 7.30, 7.28, 7.61, 6.37, 8.19, 7.54, 10.14, 8.61 and 9.38, respectively.
E0949	Mebicar	Mebicar, a derivative of bicyclic bis-ureas, inhibits the orientation reaction in albino mice, potentiates the action of narcotic hypnotics, abolishes the conditioned reflex reaction of avoidance, displays central adrenolytic activity, interferes with the norepinephrine metabolism in the brain stem.
S5496	Guanethidine Monosulfate	Guanethidine monosulfate is an antihypertensive agent that acts by inhibiting selectively transmission in post-ganglionic adrenergic nerves.
S9560	Anisodamine Hydrobromide	Anisodamine (6-Hydroxyhyoscyamine) is a naturally occurring atropine derivative and exhibits anti-inflammatory activity. It also inhibits α1-adrenergic receptors and muscarinic acetylcholine receptors (mAChRs).
S0896	DSP-4 HCl	DSP-4 hydrochloride (Neurotoxin DSP 4 (hydrochloride)) can be used for the temporary selective degradation of the central and peripheral noradrenergic neurons, which exclusively affects the noradrenergic fibers from the LC (locus coeruleus).
S5723	Carvedilol EP IMpurity E	Carvedilol is a nonselective beta blocker/alpha-1 blocker and used in management of congestive heart failure (CHF).
E4865^New	Noradrenaline bitartrate	Noradrenaline bitartrate (Norepinephrine Bitartrate) is a central nervous system (CNS) neurotransmitter and stimulator of β1 adrenergic receptors and α-adrenergic receptors, causing increased contractility and heart rate, as well as vasoconstriction.
S3764	Isoferulic Acid	Isoferulic acid (Hesperetic acid, Hesperetate, Isoferulate), a major active ingredient of Cimicifuga heracleifolia, shows anti-inflammatory, antiviral, antioxidant, and antidiabetic properties. Isoferulic acid (3-Hydroxy-4-methoxycinnamic acid) is a cinnamic acid derivative that has antidiabetic activity. Isoferulic acid binds to and activates α1-adrenergic receptors (IC50=1.4 µM) to enhance secretion of β-endorphin (EC50=52.2 nM) and increase glucose use.
E0785	YS-49	YS-49 is a PI3K/Akt (a downstream target of RhoA) activator, to reduce RhoA/PTEN activation in the 3-methylcholanthrene-treated cells, inhibits angiotensin II (Ang II)-stimulated proliferation of VSMCs via induction of heme oxygenase (HO)-1, also is an isoquinoline compound alkaloid, has a strong positive inotropic action through activation of cardiac β-adrenoceptors.	Signal Transduct Target Ther, 2024, 9(1):243
S1831	Carvedilol	Carvedilol (BM-14190, SKF 105517) is a non-selective beta blocker/alpha-1 blocker, used to treat congestive heart failure (CHF) and high blood pressure.	J Immunother Cancer, 2024, 12(11)e009805 Antioxidants (Basel), 2023, 12(8)1585 Antioxidants (Basel), 2023, 12(8)1585
S8114	Zenidolol (ICI-118551) Hydrochloride	Zenidolol (ICI-118551) Hydrochloride is a highly selective β2-adrenergic receptor antagonist with Ki values of 0.7, 49.5 and 611 nM for β2, β1 and β3 receptors, respectively.	Biomedicines, 2022, 10(2)487 iScience, 2021, 24(12):103362 Toxicol In Vitro, 2021, 77:105251
S2373	Yohimbine HCl	Yohimbine (Antagonil) has been used as a mydriatic and in the treatment of impotence. It is also alleged to be an aphrodisiac.	Anesth Analg, 2023, 137(2):426-39 Mol Pain, 2022, 18:17448069221107810 J Med Chem, 2021, 64(18):13510-13523
S1283	Asenapine maleate	Asenapine maleate (Org 5222) is a high-affinity antagonist of serotonin, norepinephrine, dopamine and histamine receptors, used for the treatment of schizophrenia and acute mania associated with bipolar disorder.	J Adv Res, 2024, S2090-1232(24)00079-1 Cell Commun Signal, 2024, 22(1):266 Mol Cancer, 2023, 22(1):136
S1549	Nebivolol hydrochloride (R-65824)	Nebivolol HCl (R-65824) selectively inhibits β1-adrenoceptor with IC50 of 0.8 nM.	J Immunother Cancer, 2024, 12(11)e009805 Oncogenesis, 2022, 11(1):24 Nat Commun, 2021, 12(1):5919
S2509	Sotalol HCl	Sotalol(MJ-1999) is a non-selective beta blocker and a potassium channel blocker with an IC50 of 43 μM.	J Immunother Cancer, 2024, 12(11)e009805 EBioMedicine, 2023, 95:104741 Toxicol Appl Pharmacol, 2021, 431:115731
S4650	Atipamezole	Atipamezole (MPV-1248, MPV1248, Antisedan) is a synthetic α2 adrenergic receptor antagonist. It has also been researched in humans as a potential anti-Parkinsonian drug.	Exp Mol Med, 2020, 10.1038/s12276-020-0461-6 Nitric Oxide, 2019, 85:1-9 Front Neurol, 2019, 10:1041
S4358	Pimozide	Pimozide (Orap, R6238) is an antagonist of Dopamine Receptors with Ki of 0.83 nM, 3.0 nM and 6600 nM for dopamine D3, D2 and D1 receptors, respectively. Pimozide also exhibits binding affinity at 5-HT1A and α1-adrenoceptor with Ki of 310 nM and 39 nM, respectively. Pimozide is an antipsychotic drug with anti-tumor activity and suppresses STAT3 and STAT5 activity.	Cell Rep Med, 2023, 10.1016/j.xcrm.2023.101286 Biol Pharm Bull, 2021, 10.1248/bpb.b21-00531
S2091	Betaxolol	Betaxolol (SL 75212,Dextrobetaxolol) is a selective beta1 adrenergic receptor blocker used in the treatment of hypertension and glaucoma.	Nat Commun, 2020, 24;11(1):1990 Chirality, 2018, 30(11):1195-1205
S5430	Metoprolol	Metoprolol is a cardioselective β1-adrenergic blocking agent with log Kd values of −7.26±0.07, −6.89±0.09, −5.16±0.12 for β1, β2, and β3 adrenoceptors, respectively. It is used for acute myocardial infarction, heart failure, angina pectoris and mild to moderate hypertension.	BMC Pharmacol Toxicol, 2024, 25(1):25 BMC Pharmacol Toxicol, 2024, 25(1):25 Cell Rep, 2022, 38(10):110468
S4817	Atenolol	Atenolol (Tenormin, Normiten, Blokium) is a selective β1 receptor antagonist with log Kd values of −6.66±0.05, −5.99±0.14, −4.11±0.07 for binding to the human β1-, β2- and β3-adrenoceptors.	Int J Mol Sci, 2022, 23(21)12948 Oncol Rep, 2021, 46(3)202
S1409	Alfuzosin HCl	Alfuzosin HCI(SL 77499 HCl) is an alpha1 receptor antagonist used to treat benign prostatic hyperplasia (BPH).	J Immunother Cancer, 2024, 12(11)e009805 Prostate, 2016, 76(8):757-66
S1424	Prazosin HCl	Prazosin HCl (cp-12299-1) is a competitive alpha-1 adrenoceptor antagonist, used to treat high blood pressure or benign prostatic hyperplasia.	J Immunother Cancer, 2024, 12(11)e009805 BMC Pharmacol Toxicol, 2020, 21(1):61
S2038	Phentolamine Mesylate	Phentolamine Mesylate(Phentolamine methanesulfonate) is a reversible and nonselective alpha-adrenergic receptor antagonist, used for the prevention or control of hypertensive episodes.	J Immunother Cancer, 2024, 12(11)e009805 Int J Mol Sci, 2024, 25(18)10162 Sci Rep, 2024, 14(1):4178
S2059	Terazosin HCl Dihydrate	Terazosin HCl is a selective α1-adrenoceptor antagonist, used for treatment of symptoms of an enlarged prostate (BPH).	J Biomed Sci, 2021, 28(1):8
S2517	Maprotiline HCl	Maprotiline HCl is a selective noradrenalin re-uptake inhibitor, used in the treatment of depression.	Front Pharmacol, 2021, 12:689767
S2126	Naftopidil	Naftopidil (KT-611) is a selective α1-adrenergic receptor antagonist with K_i of 3.7 nM, 20 nM, and 1.2 nM for α1a, α1b, and α1d, respectively, used for the treatment of benign prostatic hyperplasia.	Cell Syst, 2019, 8(2):97-108
S4123	Timolol Maleate	Timolol Maleate (MK-950,(S)-Timolol Maleate) is a non-selective, beta-adrenergic receptor antagonist for β1/β2 with K_i of 1.97 nM/2.0 nM.	J Immunother Cancer, 2024, 12(11)e009805 J Dermatolog Treat, 2020, 24:1-7
S4010	Acebutolol HCl	Acebutolol is a β-adrenergic receptors antagonist used in the treatment of hypertension, angina pectoris and cardiac arrhythmias.	Front Pharmacol, 2021, 12:740529
S1827	Betaxolol HCl	Betaxolol (SL 75212) is a β₁ adrenergic receptor blocker with IC50 of 6 μM.	J Immunother Cancer, 2024, 12(11)e009805 Chirality, 2018, 30(11):1195-1205
S4124	Tolazoline HCl	Tolazoline(Imidaline hydrochloride,NSC35110 hydrochloride) is a non-selective competitive α-adrenergic receptor antagonist.	J Immunother Cancer, 2024, 12(11)e009805 Insect Biochem Mol Biol, 2017, 90:61-70
S5942	Bisoprolol	Bisoprolol is a cardioselective β1-adrenergic blocking agent used for secondary prevention of myocardial infarction (MI), heart failure, angina pectoris and mild to moderate hypertension.	J Pathol, 2022, 10.1002/path.6020
S5337	Rauwolscine hydrochloride	Rauwolscine hydrochloride (Isoyohimbine, α-Yohimbine, corynanthidine) is the hydrochloride salt form of Rauwolscine, a specific and potent α2 antagonist with Ki of 12 nM.	J Pharm Biomed Anal, 2020, 180:113019
S3656	Piribedil	Piribedil (Trivastal, Trivastan) is a relatively selective dopamine (D2/D3) agonist with moderate antidepressant activity. It also has α2-adrenergic (α2A/α2C) antagonist properties.	Cell Rep Methods, 2023, 3(1):100381 Cell Rep Methods, 2023, 3(1):100381
E2901	(-)-Isoproterenol hydrochloride	(-)-Isoproterenol hydrochloride is an agonist of beta-adrenergic receptor. (-)-Isoproterenol hydrochloride is also used in the treatment of bradycardia; bronchodilator.	Stem Cell Res Ther, 2022, 13(1):287
S4679	Terazosin HCl	Terazosin (Hytrin, Zayasel, Terazosine, Flumarc, Fosfomic, Blavin) is a selective alpha-1 antagonist used for treatment of symptoms of an enlarged prostate (BPH). It works by blocking the action of adrenaline on smooth muscle of the bladder and the blood vessel walls.	J Immunother Cancer, 2024, 12(11)e009805 J Biomed Sci, 2021, 28(1):8
S5780	Prazosin	Prazosin is an α1-blocker that acts as an inverse agonist at alpha-1 adrenergic receptors. It is used to treat hypertension.	BMC Pharmacol Toxicol, 2020, 21(1):61
S5023	Nadolol	Nadolol (Corgard, Solgol, Anabet, SQ11725) is a non-selective beta-adrenergic antagonist with antihypertensive and antiarrhythmic activities.	J Chromatogr A, 2024, 1734:465286 Eur J Drug Metab Pharmacokinet, 2022, 10.1007/s13318-022-00780-x
S1613	Silodosin	Silodosin (KAD 3213, KMD 3213) is a highly selective α1A-adrenoceptor antagonist, used in treatment of benign prostatic hyperplasia.	J Immunother Cancer, 2024, 12(11)e009805
S2691	BMY 7378 Dihydrochloride	BMY 7378 is a multi-targeted inhibitor of α2C-adrenoceptor and α1D-adrenoceptor with pK_i of 6.54 and 8.2, respectively, and acts as a mixed agonist and antagonist for 5-HT1A receptor with pK_i of 8.3.
S1856	Metoprolol Tartrate	Metoprolol Tartrate (CGP 2175E) is a selective β1 receptor blocker medication, used to treat hypertension and heart failure.	J Immunother Cancer, 2024, 12(11)e009805
S1387	Naftopidil DiHCl	Naftopidil DiHCl (Flivas, KT-611, Avishot,BM-15275) is a selective 5-HT1A and α1-adrenergic receptor antagonist with IC50 of 0.1 μM and 0.2 μM, respectively.
S2499	Phenoxybenzamine HCl	Phenoxybenzamine HCl (NSC 37448, NCI-c01661) is a non-specific, irreversible alpha antagonist with an IC50 of 550 nM.
S2607	Buflomedil HCl	Buflomedil HCl(NSC 759291) is a vasodilator used to treat claudication or the symptoms of peripheral arterial disease; A nonselective alpha adrenergic receptor inhibitor.	J Immunother Cancer, 2024, 12(11)e009805
S5540	Landiolol hydrochloride	Landiolol hydrochloride (ONO-1101) is the hydrochloride salt form of Landiolol, which is an ultra-short-acting β1 selective adrenoceptor antagonist.
S5802	Alprenolol hydrochloride	Alprenolol hydrochloride is the hydrochloride salt form of alprenolol, which is an beta adrenergic receptorantagonist and is used as an antihypertensive, anti-anginal, and anti-arrhythmic agent.
S7538	RS-102895 Hydrochloride	RS-102895 hydrochloride (HCl) is a potent antagonist of Chemokine (C-C motif) receptor 2 (CCR2) with IC50 of 360 nM, and shows no effect on CCR1. RS-102895 hydrochloride also inhibits human α1a and α1d receptors, rat brain cortex 5-HT1a receptor in cells with IC50s of 130 nM, 320 nM, 470 nM, respectively.
S5666	Moxisylyte hydrochloride	Moxisylyte hydrochloride (thymoxamine) is an alpha-adrenergic blocking agent used for the treatment of Raynaud's disease.	J Immunother Cancer, 2024, 12(11)e009805
S5766	Alfuzosin	Alfuzosin(SL 77499), a quinazoline derivative, is a selective and competitive α1-adrenoceptor antagonist.
S0862	L-765314	L-765314 is a selective and potent α1b-adrenoceptor (α1b adrenergic receptor) antagonist with an IC50 of 1.90 nM and Kis of 5.4 and 2.0 for rat and human α1b adrenergic receptor, respectively.
E2875^New	Levobunolol(l-Bunolol) hydrochloride	Levobunolol (l-Bunolol) hydrochloride is a potent and nonselective β-adrenergic receptor antagonist with an IC50 of 48 μM.
S9285	Fargesin	Fargesin is a neolignan isolated from Magnolia plants. It is a potential β1AR antagonist through cAMP/PKA pathway.
S5789	Propafenone	Propafenone (SA-79) is an orally active sodium channel blocking agent and a beta-adrenoceptor (β-adrenergic receptor) antagonist. Propafenone offers a broad spectrum of activity in the treatment of cardiac arrhythmias.
S5965	Urapidil	Urapidil is an antihypertensive drug acting as an α1 adrenoreceptor antagonist and a 5-HT1A agonist.
S5281	Dapiprazole Hydrochloride	Dapiprazole Hydrochloride (Glamidolo Hydrochloride, Reversil Hydrochloride) is the hydrochloride salt form of dapiprazole, an alpha-adrenergic blocker used to reverse mydriasis after eye examination.
S4649	Atipamezole hydrochloride	Atipamezole (Antisedan, MPV1248) is a synthetic α2 adrenergic receptor antagonist. It has also been researched in humans as a potential anti-Parkinsonian drug. Atipamezole hydrochloride is hydrochloride form of atipamezole.
S0116	Piperoxan hydrochloride	Piperoxan hydrochloride (Benodaine, Fourneau 933, F933, DL-Piperoxan) is an antagonist of α2 (alpha 2) adrenoceptor.
S5981	S(-)-Propranolol hydrochloride	(S)-(-)-Propranolol hydrochloride, the active enantiomer of propranolol, is a β-Adrenoceptor (β-Adrenergic Receptor) antagonist with log Kd values of -8.16, -9.08, and -6.93 for β1, β2, and β3, respectively.	Heliyon, 2024, 10(11):e31865
S0812	SR59230A	SR59230A is a blood-brain barrier penetrating, potent and selective antagonist of β3-adrenergic receptor with IC50 of 40 nM, 408 nM, and 648 nM for β3, β1, and β2 receptors, respectively.
S9050	Boldine	Boldine, isolated from Peumus boldus, has alpha-adrenergic antagonist activities in vascular tissue with anti-oxidant, hepatoprotective, cytoprotective, antipyretic and anti-inflammatory effects.
S1435	Tamsulosin hydrochloride	Tamsulosin (Flomax) hydrochloride is an antagonist of alpha1A adrenoceptors in the prostate.
S4085	Levobetaxolol HCl	Levobetaxolol (AL 1577A,(S)-Betaxolol hydrochloride) exhibits a higher affinity at cloned human β1 and β2 receptors with K_i value of 0.76 nM and 32.6 nM, respectively.	J Immunother Cancer, 2024, 12(11)e009805
S5042	Bevantolol hydrochloride	Bevantolol hydrochloride (NC-1400) is a cardioselective, beta adrenoceptor antagonist, devoid of intrinsic β sympathomimetic activity and with weak membrane-stabilizing and local anesthetic properties.
S5778	Esmolol	Esmolol is a cardioselective beta1 receptor blocker with rapid onset, a very short duration of action, and no significant intrinsic sympathomimetic or membrane stabilising activity at therapeutic dosages.
E0408	JP1302	JP-1302(MMV006172), a novel highly selective α_2C-adrenoceptor antagonist with Kb of 16 nM at the α_2C-adrenoceptor subtype, also produces antidepressant and antipsychotic-like effects.
E4880^New	Labetalol	Labetalol (AH5158, Sch-15719W free base) is an orally active and selective competitive antagonist of α1-adrenergic receptors and non-selective β-adrenergic receptors. Labetalol, an anti-hypertensive agent is used in the research of cardiovascular diseases.
S4100	Esmolol HCl	Esmolol (ASL8052) is a cardioselective b-blocker, used to control rapid heartbeats or abnormal heart rhythms.	J Immunother Cancer, 2024, 12(11)e009805
S5782	Doxazosin	Doxazosin(UK 33274) is a quinazoline-derivative that selectively antagonizes postsynaptic α1-adrenergic receptors.
S2174	Hydroxyflutamide (Hydroxyniphtholide)	Hydroxyflutamide (SCH-16423, Hydroxyniphtholide) is an androgen receptor (AR) antagonist and possesses an IC50 of 0.7 μM for the androgen receptor.
S5923	Celiprolol hydrochloride	Celiprolol is a β1-adrenoceptor antagonist with partial β2 agonist activity.
S6447	Carazolol	Carazolol is a non-specific β-adrenergic receptor blocking agent and binds to β receptors irreversibly.
S5341	Metroprolol succinate	Metroprolol Succinate (Metoprolol succinate) is the succinate salt form of metoprolol, a cardioselective competitive beta-1 adrenergic receptor antagonist with antihypertensive properties and devoid of intrinsic sympathomimetic activity.
S5432	Dibenamine Hydrochloride	Dibenamine (N-(2-Chloroethyl)dibenzylamine, Sympatholytin, Dibenzylchlorethamine) is an irreversible blocker of α1 adrenoceptors.
S4278	Carteolol HCl	Carteolol HCl(Carteolol hydrochloride,OPC-1085 hydrochloride) is a β-adrenoceptor antagonist, used for the treatment of glaucoma.	J Immunother Cancer, 2024, 12(11)e009805
E0529	Metipranolol	Metipranolol (Betamann) is a potent β-adrenergic receptor antagonist, possessing the beta-blocking potencies (pA2) of 8.3, 8.4 at guinea pig atrial β1-adrenoceptor and β2-adrenoceptor of the rat uterus, respectively, also is a potent displacer of ³H-DHA binding, ligand concentration 0.7 nM, possessing a Ki value of 39 ± 24 nM.
S4291	Labetalol HCl	Labetalol HCl(AH-5158 hydrochloride,Labetalol hydrochloride,Sch-15719W) is a dual antagonist for both selective alpha1-adrenergic and nonselective beta-adrenergic receptors, used in the treatment of high blood pressure.	J Immunother Cancer, 2024, 12(11)e009805
S4797	Nicergoline	Nicergoline is an ergot derivative used to treat senile dementia and other disorders with vascular origins. It has a selective alpha-1A adrenergic receptor blocking property and also other additional mechanisms of actions.
S4009	Mirabegron	Mirabegron (YM 178) is a selective β3-adrenoceptor agonist with EC50 of 22.4 nM.	J Pers Med, 2022, 12(2)258 Hum Cell, 2022, 10.1007/s13577-022-00671-y Hum Cell, 2021, 10.1007/s13577-021-00639-4
S2521	Epinephrine bitartrate	Epinephrine bitartrate (Adrenalinium) is an alpha- and beta-adrenergic receptor stimulator.	Sci Adv, 2024, 10(33):eado1533 Int J Biol Sci, 2023, 19(7):2006-2019 Int J Biol Sci, 2023, 19(7):2006-2019
S2569	Phenylephrine HCl	Phenylephrine HCl is a selective α1-adrenergic receptor agonist, used primarily as a decongestant.	NPJ Regen Med, 2023, 8(1):9 Front Immunol, 2022, 13:1090773 Front Immunol, 2022, 10.3389/fimmu.2022.1090773
S2516	Xylazine HCl	Xylazine(BAY 1470 hydrochloride) is an α2-Adrenergic receptor agonist, used as a sedative and muscle relaxant.	J Immunother Cancer, 2024, 12(11)e009805 Cell Death Dis, 2023, 14(5):318 Eur J Pharmacol, 2021, 911:174522
S2507	Salbutamol (Albuterol) Sulfate	Salbutamol (Albuterol) Sulfate is a short-acting β2-adrenergic receptor agonist with an IC50 of 8.93 µM.	Front Physiol, 2022, 13:800055 cell, 2020, 180(1):64-78.e16 Sci Signal, 2020, 13(659)eaax0273
S2566	Isoprenaline (Isoproterenol) HCl	Isoprenaline (Isoproterenol) HCl is a non-selective beta-adrenergic receptor agonist, used for the treatment of bradycardia and heart block.	Stem Cell Res Ther, 2022, 13(1):287 BMC Cancer, 2022, 22(1):213 J Dairy Sci, 2022, 105-10:8426-8438
S9507	(−)-Norepinephrine	(−)-Norepinephrine (Arterenol, Levarterenol, L-Noradrenaline) is a natural neurotransmitter and hormone. It is an agonist of adrenergic receptors with Ki values of 330, 56, and 740 nM for α1, α2, and β1 adrenoceptors, respectively.	iScience, 2023, 26(3):106241 Commun Biol, 2022, 5(1):339 Eur J Pharmacol, 2022, 926:175040
S2090	Dexmedetomidine HCl	Dexmedetomidine HCl((+)-Medetomidine Hydrochloride) is a highly selective and potent alpha-2 adrenoceptor agonist, which reduces anesthetic requirements for patients by providing significant sedation.	Oral Dis, 2022, 10.1111/odi.14286 JHEP Rep, 2021, 3(4):100296 Sci Rep, 2021, 11(1):13345
S7974	L755507	L-755,507 is characterized as a potent and selective β3 adrenergic receptor partial agonist with EC50 of 0.43 nM. It is also recently identified to enhance CRISPR-mediated homology-directed repair (HDR) efficiency in human induced pluripotent stem cells (iPSCs) and other cell types.	Front Cell Dev Biol, 2023, 11:1276890 bioRxiv, 2023, 10.1101/2023.10.03.560773 Genesis, 2022, 60(1-2):e23465
S5527	Salmeterol	Salmeterol (Astmerole, GR-33343X, SN408D) is a long-acting beta2-adrenergic receptor agonist with Ki value of 1.5 nM for WT β2AR and shows very high selectivity for the WT β2AR(β1Ki/β2Ki ratio of approximately 1500).	Front Pharmacol, 2022, 13:865715 Mol Syst Biol, 2021, 17(8):e10239 Drug Test Anal, 2020, 10.1002/dta.2917
S5564	Xylazine	Xylazine is a partial alpha-2 adrenergic agonist that is used for sedation, anesthesia, muscle relaxation, and analgesia in animals such as horses, cattle and other non-human mammals.	Cell Death Dis, 2023, 14(5):318 Cell Death Differ, 2020, 10.1038 Mol Med Rep, 2017, 16(2):1911-1919
S5683	Isoproterenol sulfate dihydrate	Isoproterenol Sulfate is the sulfate salt form of isoproterenol, a beta-adrenergic receptor agonist with bronchodilator activity.	Stem Cell Res Ther, 2022, 13(1):287 Cell Biol Toxicol, 2021, 10.1007/s10565-021-09615-y Biochim Biophys Acta Mol Cell Res, 2021, 1868(10):119080
S4065	Guanabenz Acetate	Guanabenz Acetate (WY-8678) is an selective agonist of α2a-adrenergic receptor, α2b-adrenergic receptor and α2c-adrenergic receptor with pEC50 of 8.25, 7.01 and ~5, respectively.	Cell Stem Cell, 2020, 27(6):876-889.e12 Thyroid, 2019, 29(6):809-823
S3061	Epinephrine HCl	Epinephrine HCl (Adrenaline) is a hormone and a neurotransmitter.	Cell Rep Methods, 2023, 3(10):100599 J Immunother Cancer, 2021, 9(1)e001466
S4296	Salmeterol Xinafoate	Salmeterol Xinafoate(GR 33343X xinafoate,Salmetedur) is a long-acting β2-adrenergic receptor agonist with anti-inflammatory effects, used in the treatment of asthma symptoms and chronic obstructive pulmonary disease (COPD) symptoms.	ACS Pharmacol Transl Sci, 2019, 2(3):148-154 Commun Biol, 2018, 1:106
S3960	Higenamine hydrochloride	Higenamine (Norcoclaurine, (+-)-Demethylcoclaurine), also known as Norcoclaurine HCl, is a non-selective β2 adrenoceptor agonist which is a chemical compound naturally occurring in a number of plants.	Mol Cell Biochem, 2021, 10.1007/s11010-021-04197-z Oncol Rep, 2021, 46(3)202
S4127	Terbutaline Sulfate	Terbutaline Sulfate(Terbutaline hemisulfate) is a selective β2-adrenergic receptor agonist with IC50 of 53 nM.	BMC Pharmacol Toxicol, 2020, 21(1):61 Hum Reprod, 2016, 31(11):2506-2519
S3727	Vilanterol Trifenate	Vilanterol trifenatate (GW642444M) is a novel inhaled long-acting beta2 adrenoceptor agonist with inherent 24-hour activity for once daily treatment of COPD and asthma.	Toxicol In Vitro, 2021, 77:105251 J Neuroimmunol, 2019, 332:37-48
S5654	Indacaterol	Indacaterol is an ultra-long-acting β-adrenoceptor agonist with pKi of 7.36 for β1-adrenoceptor and pKi of 5.48 for β2-adrenoceptor.	Drug Test Anal, 2020, 10.1002/dta.2917 J Neuroimmunol, 2019, 332:37-48
S5494	Salbutamol	Salbutamol (Albuterol) is a short-acting, selective beta2-adrenergic receptor agonist used to treat or prevent bronchospasm in patients with asthma, bronchitis, emphysema, and other lung diseases.	Front Physiol, 2022, 13:800055 BMC Pharmacol Toxicol, 2020, 21(1):61
S3083	Indacaterol Maleate	Indacaterol (QAB149) is an ultra-long-acting β-adrenoceptor agonist with pK_i of 7.36 for β1-adrenoceptor and pK_i of 5.48 for β2-adrenoceptor.	J Allergy Clin Immunol, 2021, S0091-6749(21)00979-9
S2458	Clonidine HCl	Clonidine HCl(Kapvay) is a direct-acting α2 adrenergic agonist with an ED50 of 0.02±0.01 mg/kg.	J Immunother Cancer, 2024, 12(11)e009805 Mol Pain, 2022, 18:17448069221107810
S3060	Medetomidine HCl	Medetomidine is a selective α2-adrenoceptor agonist, with K_i of 1.08 nM, exhibts 1620-fold selectivity over α1-adrenoceptor.	Micromachines, 2018, 9(6)
S1437	Tizanidine HCl	Tizanidine HCl (DS 103-282) is an α2-adrenergic receptor agonist and inhibits neurotransmitter release from CNS noradrenergic neurons.	Drug Metab Dispos, 2021, 49(8):638-647
S2092	Detomidine HCl	Detomidine HCl(MPV 253AII) produce dose-dependent sedative and analgesic effects, mediatated by activation of α2 catecholamine receptors.	J Immunother Cancer, 2024, 12(11)e009805 Nature, 2018, 560(7718):372-376
S5537	Tizanidine	Tizanidine is an imidazoline derivative and a centrally acting α2 adrenergic agonist used as a muscle relaxant for therapy of acute muscle spasms and chronic spasticity.	Drug Metab Dispos, 2021, 49(8):638-647
S5768	Fenoterol hydrobromide	Fenoterol hydrobromide (Phenoterol) is the the hydrobromide salt of fenoterol, a β2 adrenoreceptor agonist with bronchodilator activity.	Toxicol In Vitro, 2021, 77:105251
S2020	Formoterol Hemifumarate	Formoterol Hemifumarate (Eformoterol, CGP 25827A, NSC 299587, YM 08316,Formoterol fumarate) is a potent, selective and long-acting β2-adrenoceptor agonist used in the management of asthma and chronic obstructive pulmonary disease(COPD).
S3041	Droxidopa	Droxidopa (L-DOPS) is a psychoactive drug and acts as a prodrug to the neurotransmitters norepinephrine (noradrenaline) and epinephrine (adrenaline).	bioRxiv, 2024, 2024.07.30.605812
S2522	L-Adrenaline	L-Adrenaline (Epinephrine) belongs to a group of the compounds known as catecholamines.This product is a hazardous chemical (acute toxicity/flammable/skin corrosive). Please use it while wearing a protective face mask, gloves, and clothing.	J Immunother Cancer, 2024, 12(11)e009805
S2519	Naphazoline HCl	Naphazoline HCl is an ocular vasoconstrictor and imidazoline derivative sympathomimetic amine.
S2533	Ritodrine HCl	Ritodrine HCl (NSC 291565,DU 21220, Ritodrine) is a hydrochloride salt of ritodrine which is a β-2 adrenergic receptor agonist.
S2438	Synephrine HCl	SynephrineHCl (Oxedrine, p-Synephrine) is a sympathomimetic α-adrenergic receptor (AR) agonist.
S3294	Demethyl-Coclaurine	Demethyl-Coclaurine (Higenamine, Norcoclaurine), the key component of the Chinese herb aconite root, is a beta-2 adrenergic receptor (β2-AR) agonist. Demethyl-Coclaurine stimulates AKT phosphorylation and requires PI3K activation for the anti-apoptotic effect in cardiomyocytes.	Signal Transduct Target Ther, 2024, 9(1):243
S2545	Scopine	Scopine(6,7-Epoxytropine) is the metabolite of anisodine, which is a α1-adrenergic receptor agonist and used in the treatment of acute circulatory shock.
S2523	DL-Adrenaline	DL-Adrenaline(dl-Epinephrine) is a hormone and a neurotransmitter secreted by the medulla of the adrenal glands.
S4266	Brimonidine Tartrate	Brimonidine Tartrate(UK 1434 Tartrate) is a highly selective α-adrenergic receptor agonist with EC50 of 0.45 nM for the α2A adrenoreceptor, and used to treat open-angle glaucoma or ocular hypertension.
S2615	Noradrenaline bitartrate monohydrate	Noradrenaline bitartrate monohydrate (Levophed) is a direct alpha-adrenergic receptors stimulator.
S0032	Batefenterol	Batefenterol (GSK961081, TD-5959) is both a muscarinic receptor antagonist and a β2-adrenoceptor agonist with Ki of 1.4 nM, 1.3 nM and 3.7 nM for hM2, hM3 muscarinic receptors and hβ2-adrenoceptor, respectively.
E4888^New	Guanabenz hydrochloride	Guanabenz hydrochloride(NE56490) is a small molecule, antihypertensive agonist of α2-adrenoceptor. It also inhibits eIF2α and GADD34, showing potential for treating cardiac hypertrophy, heart failure, atherosclerosis, and ischemic heart disease.
E4825^New	Naphazoline (nitrate)	Naphazoline (nitrate) is a agonist of peripheral α2-adrenergic receptor and used as a topical decongestant. It also acts as a vasoconstrictor that effectively reduces intraoperative bleeding and enhances postoperative analgesia. When used in conjunction with intranasal lidocaine, it significantly reduces both intra- and postoperative pain, thereby decreasing the need for rescue analgesics in the postoperative period following septorhinoplasty.
S5769	Fenoterol	Fenoterol (Phenoterol) is a β2 adrenoreceptor agonist with bronchodilator activity.
S4135	Clorprenaline HCl	Clorprenaline HCl (NSC 334693) is a β2-receptor agonist, it has a significant expansion of the bronchial effect.
S4043	Tetrahydrozoline HCl	Tetrahydrozoline (Tetryzoline) HCl is an imidazoline derivative with alpha receptor agonist activity.
E4963^New	Clonidine	Clonidine(Clonidin) is a direct-acting α2-adrenergic agonist. It is potentially used in the treatment of attention-deficit hyperactivity disorder (ADHD) in children and adolescents.
S5217	Arformoterol Tartrate	Arformoterol Tartrate is the tartrate salt of arformoterol, a long-acting beta-2 adrenergic agonist with bronchodilator activity.
S5734	Midodrine hydrochloride	Midodrine hydrochloride is the hydrochloride salt form of midodrine, an adrenergic alpha-1 agonist used as a vasopressor.
S5735	Midodrine	Midodrine belongs to the class of medications known as vasopressors. It is an adrenergic alpha-1 agonist.
S5727	Tetryzoline	Tetryzoline (Tetrahydrozoline) is an alpha-adrenergic agonist used in some over-the-counter eye drops and nasal sprays.
S5954	L-(-)-α-Methyldopa hydrate	L-(-)-α-Methyldopa (Methyldopa, MK-351) hydrate, a potent antihypertensive drug, is a selective agonist for α2-adrenergic receptors.
E4842^New	Vilanterol	Vilanterol (GW642444) is a potent and selective agonist of β2-adrenoceptor (β2-AR) with pEC50 of β2-AR, β1-AR, and β3-AR is 10.37, 6.98 and 7.36 respectively in cAMP detection assays.
S2576	Xylometazoline HCl	Xylometazoline is an α-adrenoceptor agonist commonly used as nasal decongestant, exhibits highest potency at α_2B-adrenoceptor subtype with EC50 of 99 μM.
S3640	Methoxyphenamine Hydrochloride	Methoxyphenamine Hydrochloride (2-methoxy-N-methylamphetamine, OMMA) is a β-adrenergic receptor agonist of the amphetamine class used as a bronchodilator.
S2304	Gramine	Gramine (Donaxine) is a natural indole alkaloid isolated from giant reed, acts as an active adiponectin receptor (AdipoR) agonist, with IC50 of 3.2 µM and 4.2 µM for AdipoR2 and AdipoR1, respectively. Gramine is also a human and mouse β2-Adrenergic receptor (β2-AR) agonist.
S1423	Dobutamine HCl	Dobutamine(Dobutrex) hydrochloride is a selective potent agonist of β1-AR (β-1 adrenergic receptor) and exhibits weak activity at α1-AR and β2-AR. Dobutamine is a sympathomimetic compound that effectively restores blood pressure in hypotensive dogs and human patients by improving myocardial contractility and increasing cardiac output (CO).
S6583	Apraclonidine HCl	Apraclonidine (Iopidine,ALO 2145) is a sympathomimetic used in glaucoma therapy. It is an alpha2-adrenergic agonist.
S4485	Olodaterol	Olodaterol is a long-acting β2-adrenergic receptor agonist that is used as a component of an inhalation (Tiotropium/Olodaterol) for treating patients with chronic obstructive pulmonary disease (COPD).
S4693	Guanfacine Hydrochloride	Guanfacine Hydrochloride (Tenex, Intuniv) is a selective α2A-adrenoceptor agonist with anti-hypertensive effect.	J Immunother Cancer, 2024, 12(11)e009805
S5669	Isoxsuprine hydrochloride	Isoxsuprine hydrochloride is a beta-adrenergic agonist with vasodilator activity.
S5925	Olodaterol hydrochloride	Olodaterol hydrochloride (BI-1744) is the hydrochloride salt form of Olodaterol, which is a long-acting beta2-adrenergic agonist.
E1049^New	CL316243	CL316243 is a highly potent and selective agonist of β3-adrenoceptor with an EC50 value of 3 nM, respectively but is an extremely poor to β1/2- receptors.It effectively stimulates adipocyte lipolysis and increases brown adipose tissue thermogenesis and metabolic rate.
S6407	Tulobuterol hydrochloride	Tulobuterol is a long-acting β2-adrenergic receptor agonist that has bronchodilatory, anti-inflammatory, and antiviral activities.
E4892^New	Formoterol	Formoterol is a highly selective and potent long-acting beta2-adrenergic agonist that functions by binding to and activating beta2-adrenergic receptors on the smooth muscle cells of the airways. It is used in the treatment of patients with chronic obstructive pulmonary disease (COPD).
E2944	Norepinephrine hydrochloride	Norepinephrine (Levarterenol; L-Noradrenaline) hydrochloride is a potent agonist of adrenergic receptor (AR). Norepinephrine activates α1, α2, β1 receptors.
E4849^New	Terbutaline	Terbutaline(Brican, Brethine), an active metabolite of bambuterol is an orally active agonist of β2-adrenergic receptor, that increases MKP-1 expression. Terbutaline is used in the treatment of obstructive lung diseases as a bronchodilator remedy. It also exhibits anti-inflammatory effects.
S2083	Procaterol HCl	Procaterol HCl (OPC-2009) is a short-acting β2-adrenergic receptor agonist with K_p of 8 nM, used for the treatment of asthma
E2964	Norepinephrine tartrate	Norepinephrine tartrate is a potent agonist of adrenergic receptor (AR). Norepinephrine activates α1, α2, β1 receptors.
S4277	Bambuterol HCl	Bambuterol HCl(Bambuterol hydrochloride,KWD-2183 hydrochloride) is a potent β-adrenoceptor agonist, used in the treatment of asthma.
E1746^New	Protokylol hydrochloride	Protokylol hydrochloride(Caytine hydrochloride, JB-251 hydrochloride) is a salt form of protokylol and is an agonist of β-adrenergic receptor. Protokylol hydrochloride is also used as a bronchodilator.
S5750	DL-Norepinephrine hydrochloride	Norepinephrine (noradrenaline) is the neurotransmitter at most sympathetic neuroeffector junctions and has pharmacologic effects on both α1 and β1 adrenoceptors.
S2362	Synephrine	Synephrine (Oxedrine), a natural protoalkaloid in the extract of bitter orange and other citrus species, is commonly used for weight loss.
S9508	Brimonidine	Brimonidine (Bromoxidine, UK 1430) is an alpha adrenergic receptor agonist (primarily alpha-2) and is used for the treatment of open-angle glaucoma or ocular hypertension to lower intraocular pressure.
S5267	Nylidrin Hydrochloride	Nylidrin Hydrochloride (Buphenine), a β-adrenergic agonist, is used therapeutically for its vasodilating effect on the peripheral circulation and possibly on the cerebral circulation as well.
S6487	fluticasone furoate	Fluticasone furoate (GW685698) is an inhaled corticosteroid/long-acting beta-agonist combination with a prolonged bronchodilator duration of action. It is used for the treatment of non-allergic and allergic rhinitis administered by a nasal spray.
S3185	Adrenalone HCl	Adrenalone is an adrenergic agonist used as a topical vasoconstrictor and hemostatic, mainly acts on alpha-1 adrenergic receptors.	J Immunother Cancer, 2024, 12(11)e009805
S4481	Guanabenz	Guanabenz (GBZ, GA, Wytensin, Wy-8678,BR-750) is an orally active central alpha 2-adrenoceptor (α2 adrenergic receptor) agonist with antihypertensive action.
S3153	Levalbuterol tartrate	Levalbuterol tartrate(Levosalbutamol tartrate) is a relatively selective beta2-adrenergic receptor agonist used for the treatment of asthma.	J Immunother Cancer, 2024, 12(11)e009805
E4888^New	Guanabenz hydrochloride	Guanabenz hydrochloride(NE56490) is a small molecule, antihypertensive agonist of α2-adrenoceptor. It also inhibits eIF2α and GADD34, showing potential for treating cardiac hypertrophy, heart failure, atherosclerosis, and ischemic heart disease.
E4825^New	Naphazoline (nitrate)	Naphazoline (nitrate) is a agonist of peripheral α2-adrenergic receptor and used as a topical decongestant. It also acts as a vasoconstrictor that effectively reduces intraoperative bleeding and enhances postoperative analgesia. When used in conjunction with intranasal lidocaine, it significantly reduces both intra- and postoperative pain, thereby decreasing the need for rescue analgesics in the postoperative period following septorhinoplasty.
E4865^New	Noradrenaline bitartrate	Noradrenaline bitartrate (Norepinephrine Bitartrate) is a central nervous system (CNS) neurotransmitter and stimulator of β1 adrenergic receptors and α-adrenergic receptors, causing increased contractility and heart rate, as well as vasoconstriction.
E2875^New	Levobunolol(l-Bunolol) hydrochloride	Levobunolol (l-Bunolol) hydrochloride is a potent and nonselective β-adrenergic receptor antagonist with an IC50 of 48 μM.
E4963^New	Clonidine	Clonidine(Clonidin) is a direct-acting α2-adrenergic agonist. It is potentially used in the treatment of attention-deficit hyperactivity disorder (ADHD) in children and adolescents.
E4842^New	Vilanterol	Vilanterol (GW642444) is a potent and selective agonist of β2-adrenoceptor (β2-AR) with pEC50 of β2-AR, β1-AR, and β3-AR is 10.37, 6.98 and 7.36 respectively in cAMP detection assays.
E1049^New	CL316243	CL316243 is a highly potent and selective agonist of β3-adrenoceptor with an EC50 value of 3 nM, respectively but is an extremely poor to β1/2- receptors.It effectively stimulates adipocyte lipolysis and increases brown adipose tissue thermogenesis and metabolic rate.
E4880^New	Labetalol	Labetalol (AH5158, Sch-15719W free base) is an orally active and selective competitive antagonist of α1-adrenergic receptors and non-selective β-adrenergic receptors. Labetalol, an anti-hypertensive agent is used in the research of cardiovascular diseases.
E4892^New	Formoterol	Formoterol is a highly selective and potent long-acting beta2-adrenergic agonist that functions by binding to and activating beta2-adrenergic receptors on the smooth muscle cells of the airways. It is used in the treatment of patients with chronic obstructive pulmonary disease (COPD).
E4849^New	Terbutaline	Terbutaline(Brican, Brethine), an active metabolite of bambuterol is an orally active agonist of β2-adrenergic receptor, that increases MKP-1 expression. Terbutaline is used in the treatment of obstructive lung diseases as a bronchodilator remedy. It also exhibits anti-inflammatory effects.
E1746^New	Protokylol hydrochloride	Protokylol hydrochloride(Caytine hydrochloride, JB-251 hydrochloride) is a salt form of protokylol and is an agonist of β-adrenergic receptor. Protokylol hydrochloride is also used as a bronchodilator.

Choose Selective Adrenergic Receptor Inhibitors